「ボリンジャーバンド」をひとことで言うよ
ボリンジャーバンドとは、
統計学の観点から、株価がウロウロしうる範囲を
グラフにしたもの
です。
ボリンジャーバンドとは?
ボリンジャーバンドは、
統計学の観点から、株価がウロウロしうる範囲を
グラフにしたもの
です。
主にチャートといっしょに表示して使うグラフです。
基本の見かた
「ボリンジャーバンドとは何か」の前に、
まずは実物を見てみましょう。
今、むずかしそうと思っても大丈夫。
この記事を読み終わるときには、
なんなく見れるようになってます。
ボリンジャーバンドは、こんなグラフです。
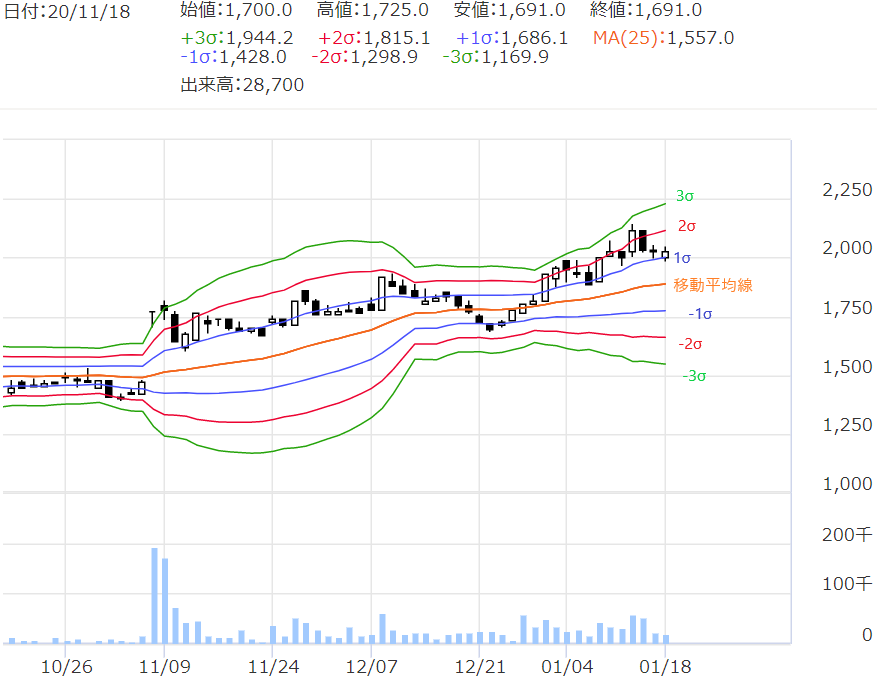

オレンジ色の線が真ん中にあって、
その上下に青の線、赤の線、緑の線が
それぞれあるね。
次は、おなじ色の線の幅をそれぞれ見てください。
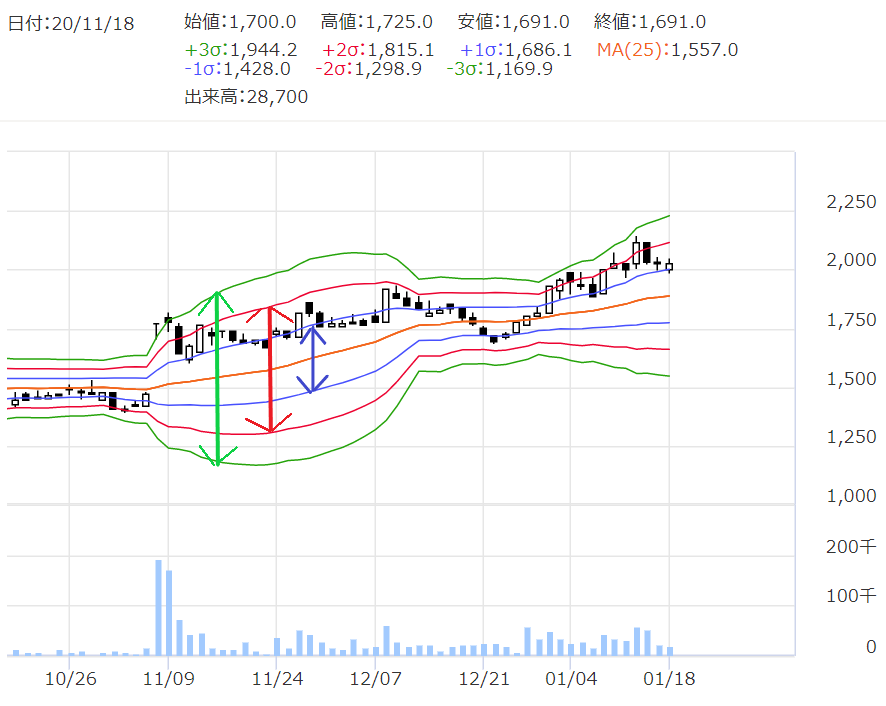
この幅が、
統計学上、株価がウロウロしうる幅
です。
青の幅(1σ~-1σ)では、
今までの株価の68%がウロウロしています。
赤の幅(2σ~-2σ)では、
今までの株価の95%がウロウロしています。
緑の幅(3σ~-3σ)では、
今までの株価の99%がウロウロしています。

たしかに…チャートを見ても、
だいたいそんな感じになってる。
これが、基本の見かたです。
これだけ知っていれば、
ボリンジャーバンドはひとまず大丈夫。
ボリンジャーバンドのグラフに、
これ以上の情報はありません。

いや、でも、何このグラフ?
何を表してんの?
ボリンジャーバンドは、
株価の「標準偏差」をグラフにしたもの。
ここからはボリンジャーバンドをもっと詳しく知りたい人向けです。
ボリンジャーバンドの説明の前に、
「標準偏差ってなに?」を説明しますね。
標準偏差とは、「データのばらつき度」を
表した数です。
「σ」(シグマ)という記号で表されます。
たとえば、とある学校の数学のテスト。
学年の平均点が60点、標準偏差が「3」
だったとします。
このとき、統計学では、
すべての点数のうち68%は、
平均点60点±3点の間にある
という考え方をします。
つまり、
その学年の生徒の68%は、
数学の点数が、
57点~63点の間におさまっている
ということです。

そして、
平均点に標準偏差を2倍したものを足し引きすると、
その数字の間には、
すべてのデータの95%の数値が入っています。
さっきの数学の点数でいうと、
60点±6点(標準偏差3の2倍)
つまり、
54点~66点の間には、
なんと学年全体の95%もの人の
数学の点数が収まっている、
ということです。

あっ、さっきの図の「1σ」「-2σ」って、
そういうことか!!
そうです。これが先ほどの図。
〇で囲った部分に、「1σ」「-2σ」って書いてます。
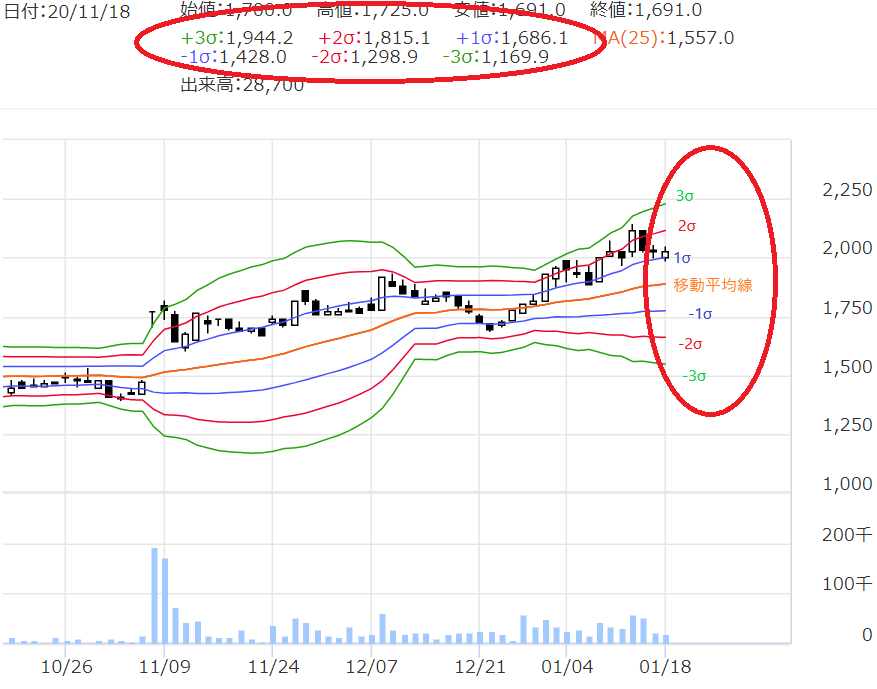
ボリンジャーバンドは、
この標準偏差の考え方を、
株価に応用したものなんです。
いままでの株価の68%は、
株価の平均±標準偏差×1倍
の間におさまっています。
その幅を表したのが、
2本の青い線の幅です。
同じように、
今までの株価の95%は、
株価の平均±標準偏差×2倍
の間におさまっていて、
その幅をあらわしたのが、
2本の赤い線の幅です。

ということは、平均±標準偏差の3倍
の数値の間には、
すべてのデータの99%がおさまってる
ってことか。
そうです。
株価もテストの点数もそれは変わりません。
その幅を表したのが、
2本の緑の線ってことです。
ボリンジャーバンドの使い方
最後に、ボリンジャーバンドの、
トレードの中での使い方について触れておきます。
先ほども言いましたが、
ボリンジャーバンドは、
統計学上、株価がウロウロしうる範囲
以外の情報はありません。
ただ、
やっぱり株価が3σの線、-3σの線に近づくと、
今までの傾向とくらべて、
売られすぎ、買われすぎ
と判断できます。
そこを売りどき、買いどきと判断するのは、
合理的です。
あとオススメなのは、
株価が+3σの線を越えたとき、
その銘柄を調べに行くこと
ですね。

+3σの線を越えるってことは、
99%あり得ない値をつけた
ってこと。
ぜったい、その銘柄とか、
その銘柄のまわりの環境で、
なにか変化が起きてるってことだよ。
そういう銘柄は、大きく株価が変動します。
面白いことが起こるかもしれませんね。
まとめるよ
- ボリンジャーバンドは、統計学上、株価がウロウロしうる範囲を表したグラフ。
- それ以上の意味はない。
- ±3σに近づいたときは注意





統計の考え方を株価に応用したものだよ。